Геометрические задачи.

Задача №1

На рис. 1 изображена окружность, в ней три отрезка: CD - хорда этой окружности и отрезки AB и BC. Точки A, C и D лежат на окружности. Все три отрезка известной длины. Смежные отрезки попарно перпендикулярны: отрезок AB перпендикулярен отрезку BC, а отрезок BC перпендикулярен отрезку CD. Требуется найти радиус окружности.

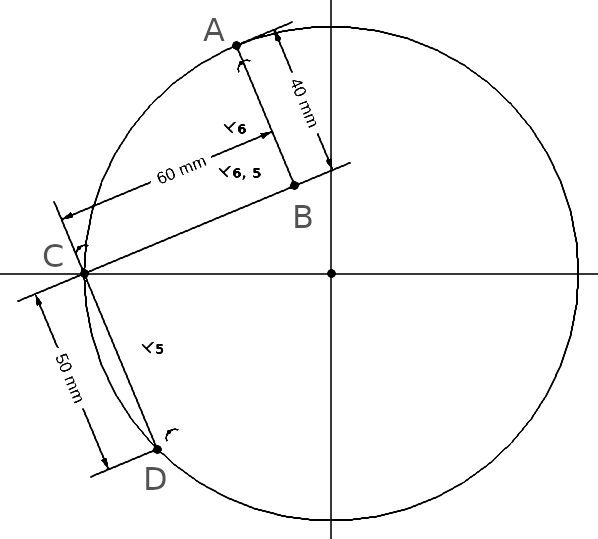
Рис. 1. Задача на нахождение радиуса окружности.

Решение

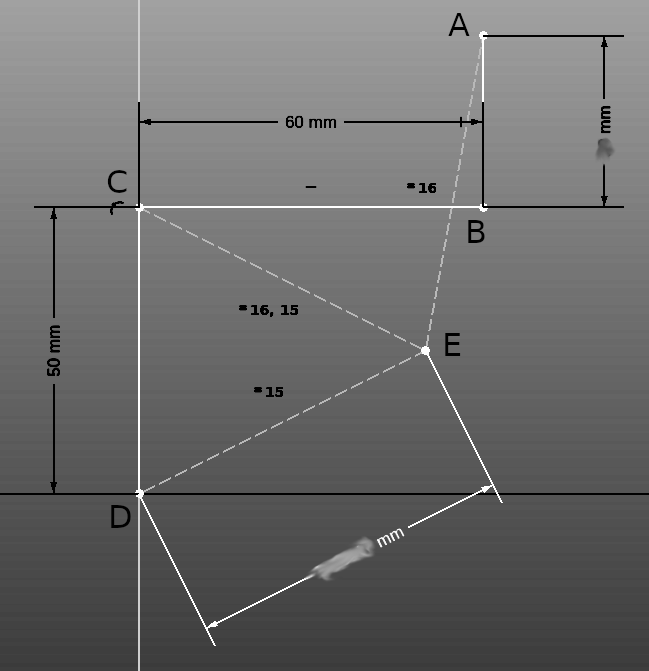
Рис. 2. Рисунок 1 из задачи 1 с дополнительными построениями.

На рисунке 2 пунктирными линиями обозначены радиусы окружности из рисунка 1.

Решение задачи 1 будет представлено в векторной форме.

Координаты векторов:

DC = (0, 50)

CB = (60, 0)

BA = (0, 40)

DE = (X₁, 25)

EC = (-X₁, 25)

EA = (X₂, 90-25) = (X₂, 65)

Длины векторов:

|DE| = √(X₁² + 25²)

|EA| = √(X₂² +65²)

|DE| = |EA|

X₁² +25² = X₂² +65²

DE + EA = (X₁ + X₂, 90)

DC + CB + BA = (60, 90)

X₁ + X₂ = 60

Система уравнений:

X₁ + X₂ = 60

X₁² + 25² = X₂² + 65²

X₁ = √(X₂² + 65² -25²)

√(X₂² + 65² -25²) + X₂ = 60

X₂² + 65² -25² = (60 - X₂)²

X₂² + 65² -25² = 60² - 120X₂ +X₂²

65² -25² = 60² - 120X₂

120X₂ = 60² +25² -65²

120X₂ = 0

X₂ = 0

X₁ = 60

|DE| = √(X₁² + 25²) = √(60² + 25²) = √4225 = 65

Ответ: Радиус окружности равен 65 мм.