Головоломка Ханойские башни на Python

Имеется три стержня a, b и c. На стержень а нанизаны пирамидкой несколько колец разного диаметра. Задача состоит в том, чтобы за наименьшее число ходов перенести пирамиду на стержень b, используя стержень c, как вспомогательный.

За один раз разрешается переносить только одно кольцо, причём, нельзя класть большее кольцо на меньшее.

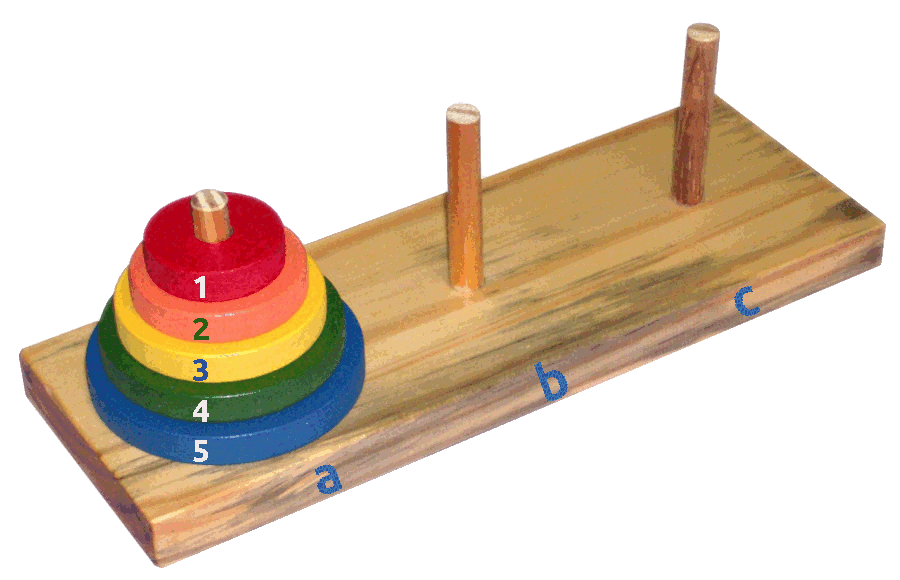
Рис. 1. Головоломка "Ханойские башни" с пятью кольцами.

Решить головоломку Ханойская башня можно несколькими методами.

Рекурсивный метод.

Предположим, что нам известен алгоритм перемещения n-1 дисков с одного стержня на второй, тогда функция play() для перемещения n дисков со стержня surse на стержень receiver должна будет:

переместить n-1 диск со стержня surse на стержень storage
последний диск n переместить со стержня surse на стержень receiver
переместить n-1 диск со стержня storage на стержень receiver.

n = 5                                           # Количество дисков

def play(n, sourse, receiver, storage):
    """
    Функция перемещения n дисков в головоломке Ханойская башня.
    Аргументы функции:
    Первый аргумент n - integer (целое число), количество дисков в пирамиде.
    sourse, receiver, storage - любого типа.
    Второй аргумент - sourse, стержень с которого перекладываем диски.
    Третий аргумент - receiver, стержень на который перекладываем диски.
    Четвёртый аргумент - storage, стержень на который перекладываем n-1 дисков
    для временного хранения в процессе общей работы.
    """
    if n <= 0: return
    play(n-1, sourse, storage, receiver)
    print("Диск ", n, " : ", sourse, " --> ", receiver)
    play(n-1, storage, receiver, sourse)

play (n, 'a', 'b', 'c')

Лист. 1. Программа, решающая головоломку Ханойская башня.

Диск  1  :  a  -->  b
Диск  2  :  a  -->  c
Диск  1  :  b  -->  c
Диск  3  :  a  -->  b
Диск  1  :  c  -->  a
Диск  2  :  c  -->  b
Диск  1  :  a  -->  b
Диск  4  :  a  -->  c
Диск  1  :  b  -->  c
Диск  2  :  b  -->  a
Диск  1  :  c  -->  a
Диск  3  :  b  -->  c
Диск  1  :  a  -->  b
Диск  2  :  a  -->  c
Диск  1  :  b  -->  c
Диск  5  :  a  -->  b
Диск  1  :  c  -->  a
Диск  2  :  c  -->  b
Диск  1  :  a  -->  b
Диск  3  :  c  -->  a
Диск  1  :  b  -->  c
Диск  2  :  b  -->  a
Диск  1  :  c  -->  a
Диск  4  :  c  -->  b
Диск  1  :  a  -->  b
Диск  2  :  a  -->  c
Диск  1  :  b  -->  c
Диск  3  :  a  -->  b
Диск  1  :  c  -->  a
Диск  2  :  c  -->  b
Диск  1  :  a  -->  b

Лист. 2. Результат работы программы решающей головоломку Ханойская башня с пятью дисками.

Тот кто придумал этот алгоритм — гений!

Не трудно заметить, что минимальное число ходов, необходимое для решения головоломки, равно (2ⁿ − 1), где n — число дисков.

Python