Ханойские башни, игра

Эта головоломка была изобретена французским математиком Эдуардом Лукасом в 1883 году. Она продавалась с 8 дисками и с описанием легенды о том, что в храме в Бенаресе, Индия, есть "Башня Брахмы", где жрецы храма перемещают 64 золотых диска по одному диску каждую секунду. Когда они выполнят свою работу, миру придет конец.

Правила игры

Имеется три стержня X, Y и Z. На стержень источник X (source) нанизаны пирамидкой несколько колец разного диаметра. Задача состоит в том, чтобы за наименьшее число ходов перенести пирамиду на стержень целевой Y (target), используя стержень резервный Z (storage), как вспомогательный.

За один раз разрешается переносить только одно кольцо, причём, нельзя класть большее кольцо на меньшее.

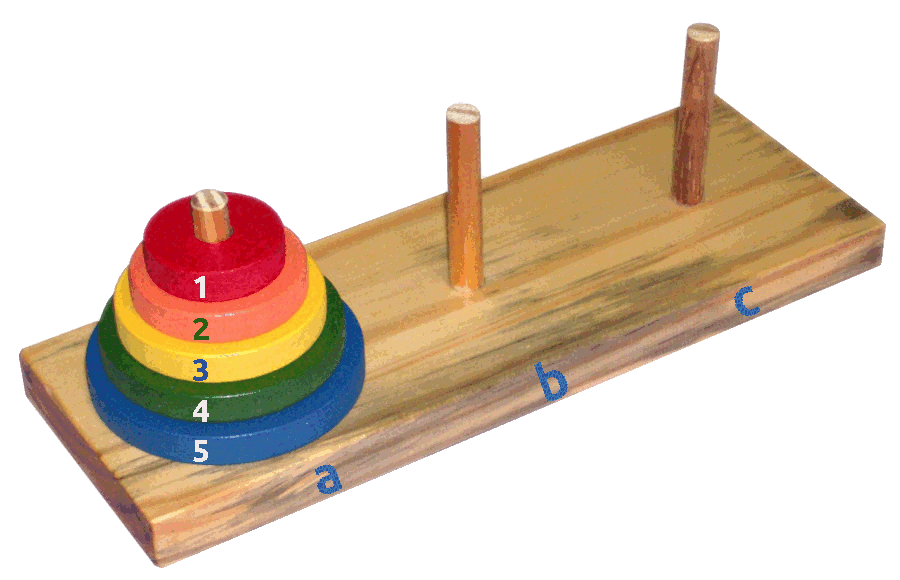
Рис. 1. Головоломка "Ханойские башни" с пятью кольцами.

Решить головоломку Ханойская башня можно несколькими методами.

Рекурсивный метод

Предположим, что нам известен алгоритм перемещения n-1 дисков с одного стержня на второй, тогда функция play() для перемещения n дисков со стержня surse на стержень target должна будет:

переместить n-1 диск со стержня surse на стержень storage
последний диск n переместить со стержня surse на стержень target
переместить n-1 диск со стержня storage на стержень surse.

На печать выводим перемещение n-го диска.

def play(n, x, y, z):
    print('диск ', n, x, '->', y)

n = 4      # Количество дисков
board = (' стержень X', ' стержень Y', ' стержень Z')
play(n, *board)

Лист. 1. Программа перемещения последнего, n-го диска.

диск  4  стержень X ->  стержень Y

Лист. 2. Вывод программы листинг 1.

Если мы будем решать задачу рекурсивно, нам необходимо предусмотреть выход из рекурсии. То есть, мы должны определить границу для рекурсии.

Рекурсия должна закончиться, когда последний диск будет установлен на целевой стержень, а на двух других стержнях не останется дисков. То есть, если n — это количество дисков, которые надо переложить, то рекурсия и игра заканчивается, когда n = 0.

def play(n, x, y, z):
    '''
    n количество дисков
    x стержень источник
    y целевой стержень
    z промежуточный стержень
    '''
    if n==0:
        return
    play(n-1, x, z, y)
    print('диск ', n, x, '->', y)
    play(n-1, z, y, x)

n = 4      # Количество дисков
board = (' стержень X', ' стержень Y', ' стержень Z')
play(n, *board)

Лист. 3. Программа игры Ханойская башня.

диск  1  стержень X ->  стержень Z
диск  2  стержень X ->  стержень Y
диск  1  стержень Z ->  стержень Y
диск  3  стержень X ->  стержень Z
диск  1  стержень Y ->  стержень X
диск  2  стержень Y ->  стержень Z
диск  1  стержень X ->  стержень Z
диск  4  стержень X ->  стержень Y
диск  1  стержень Z ->  стержень Y
диск  2  стержень Z ->  стержень X
диск  1  стержень Y ->  стержень X
диск  3  стержень Z ->  стержень Y
диск  1  стержень X ->  стержень Z
диск  2  стержень X ->  стержень Y
диск  1  стержень Z ->  стержень Y

Лист.4. Вывод программы листинг 3.

def play(n, x, y, z):
    '''
    n number of disks
    x rod source
    y target rod
    z storage rod
    '''
    if n==0:
        return
    play(n-1, x, z, y)
    print('disk ', n, x, '->', y)
    play(n-1, z, y, x)

n = 4      # Number of disks
board = (' rod X', ' rod Y', ' rod Z')
play(n, *board)

Sketch 1. Program of the game Hanoi Tower.

disk  1  rod X ->  rod Z
disk  2  rod X ->  rod Y
disk  1  rod Z ->  rod Y
disk  3  rod X ->  rod Z
disk  1  rod Y ->  rod X
disk  2  rod Y ->  rod Z
disk  1  rod X ->  rod Z
disk  4  rod X ->  rod Y
disk  1  rod Z ->  rod Y
disk  2  rod Z ->  rod X
disk  1  rod Y ->  rod X
disk  3  rod Z ->  rod Y
disk  1  rod X ->  rod Z
disk  2  rod X ->  rod Y
disk  1  rod Z ->  rod Y

Sketch 2.

Программирование GUI

Виртуальное игровое поле playArea состоит из списка позиций на всех трёх пирамидах. Следовательно, оно содержит в три раза больше элементов чем одна пирамида. Каждая треть списка playArea отображает состояние одной из трёх пирамид. Каждая треть списка playArea организована в виде стека LIFO (англ. Last In, First Out – «последним пришёл — первым ушёл») с основаниями в начале каждой трети списка playArea. Напомним, что по правилам игры, на вершине пирамиды всегда находится наименьший диск, в основании, соответственно, наибольший на этом стержне.

Python